Grafuri neorientate

Terminologie

Definiție

Graf neorientat = un graf $G=(V,E)$ în care relația binară este simetrică: $\forall (v,w)\in E\to \exists (w,v)\in E$

Nod

Nod = element al mulțimii $V$, unde $G=(V,E)$ este un graf neorientat

Nod izolat

Un nod cu gradul 0

Nod terminal

Un nod cu gradul 1

Muchie

Muchie = element al mulțimii $E$ ce descrie o relație existentă între două noduri, unde $G=(V,E)$ este un graf neorientat Muchiile sunt considerate ca neavând direcție deci pot fi parcurse în ambele sensuri.

Adiacența

Vârfurile $w$ și $v$ sunt adiacente dacă $(v,w)\in E$. În cazul grafurilor neorientate această relație este bidirecțională deci $w$ adiacent cu $v$ $\leftrightarrow$ $v$ adiacent cu $w$.

Incidența

O muchie este incidentă cu un nod dacă îl are pe acesta ca extremitate. Muchia $(v,w)$ este incidentă cu $v$ respectiv $w$.

Grad

Gradul unui nod $v$, dintr-un graf neorientat, este numărul natural ce reprezintă numărul de noduri adiacente cu acesta, sau numărul de muchii incidente.

Lanț

Lanțul este o serie de noduri dintr-un graf neorientat $G=(V,E)$ cu proprietatea ca între oricare 2 noduri sunt adiacente (există o muchie). $w_1,w_2,w_3,...,w_n$ cu proprietatea că $(w_i,w_{i+1})\in E,1\le i<n$ Proprietățile lanțurilor și tipurile lor sunt similare cu cele ale drumurilor.

Lungimea unui lanț

Lungimea unui lanț este numărul de muchii (sau $\text{numa˘rul de noduri}-1$) din care acesta este format.

Lanț simplu

Lanțul simplu este lanțul care conține numai muchii distincte.

Lanț compus

Lanțul compus este lanțul care nu este format numai din muchii distincte. Practic, dacă un lanț nu este simplu, este compus.

Lanț elementar

Este un lanț în care nu se repetă niciun nod, și implicit nicio muchie. Deci practic un lanț elementar este un lanț simplu, dar nu și invers. Lanțul $(1,2,3,4,2,5)$ este simplu dar nu este elementar, dar lanțul $(1,2,3,4)$ este atât simplu cât și elementar.

Ciclu

Un ciclu este un lanț în care primul nod coincide cu ultimul.

Lungimea unui ciclu

Lungimea unui ciclu, la fel ca lungimea unui lanț este egală cu numărul de muchii. Lungimea unui ciclu nu poate fi 2.

Ciclu simplu

Un ciclu simplu, la fel ca un lanț simplu este un ciclu în care nu se repetă nici o muchie.

Ciclu compus

Ciclul compus este ciclul care nu este format numai din muchii distincte. Practic, dacă un ciclu nu este simplu, este compus. Ciclul $(1,2,3,4,5,3,2,6,1)$ este compus deoarece se repetă muchia $(2,3)$

Ciclu elementar

Un ciclu este elementar dacă este format doar din noduri distincte, excepție făcând primul și ultimul. Implicit asta înseamnă că nu se repetă nici o muchie. Deci orice ciclu elementar este implicit și ciclu simplu, dar nu și invers. Ciclul $(1,2,3,4,2,5,1)$ este simplu dar nu este și elementar, dar ciclul $(1,2,5)$ este atât simplu cât și elementar.

Tipuri de grafuri neorientate

Graf regulat

Graful regulat este graful în care toate nodurile au același grad. Deci și un graf fără muchii $G=(V,\varnothing )$ este graf regulat.

Graf complet

Graful complet este un graf în care există o muchie între oricare 2 noduri. Numărul de muchii ale unui graf complet este $C_n^2=\frac{n(n-1)}{2}=$, unde $n$ este numărul de muchii.

Graf nul

$G=(V,\varnothing )$ Graful nul este graful în care nu există muchii/arce, sau în care mulțimea muchiilor este vidă $E=\varnothing$. A nu fi confundat cu cu graful vid. Graful complementar al grafului nul este graful complet

Graf complementar

Fie $G=(V,E)$ un graf. Se numește graf complementar al grafului $G$, graful $G^{\prime }=(V,E^{\prime })$ cu proprietatea că două noduri $i$ și $j$ sunt adiacente în $G^{\prime }$ dacă și numai dacă nu sunt adiacente în $G$. Cu alte cuvinte, dacă am considera graful complet $G=(V,E^{\prime \prime })$ , $E^{\prime }\cap E=\varnothing \text{și}{E}^{\prime }\cup E=E^{\prime \prime }$

Graf regulat

Un graf neorientat este numit regulat dacă toate nodurile au același grad.

Graf bipartit

Un graf $G=(V,E)$ este numit bipartit dacă există 2 mulțimi nevide, $A$ și $B$ astfel încât $V=A\cup B,A\cap B=\varnothing$ și orice muchie $u\in E$ a lui $G$ are o extremitate în $A$, iar cealaltă în $B$. Mulțimile $A$ și $B$ formează o partiție a lui $V$. Exemplu: Graful următor este bipartit: $A=\{1,2,5,7\}$ și $B=\{3,4,6\}$

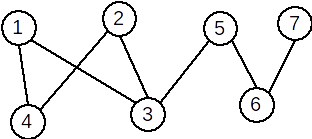
Graf bipartit complet

Un graf bipartit $G=(V,E)$ este numit bipartit complet dacă pentru oricare 2 noduri $x\in A,y\in B$ există în graf muchia $(x,y)\in E$. Exemplu: graful următor este bipartit complet.

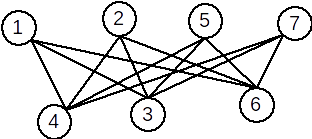
Arbore

Se numește arbore un graf conex și aciclic.

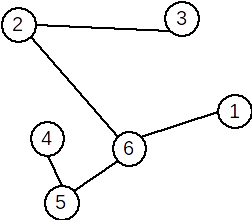
• Un graf parțial care este arbore se numește arbore parțial.
• Un graf care nu conține cicluri se mai numește pădure. Într-o pădure fiecare componentă conexă este un arbore. Vezi articoulul despre arbori pentru mai multe detalii.

Graf neorientat hamiltonian

• Lanțul elementar care conține toate nodurile se numește hamiltonian.
• Ciclul elementar care conține toate nodurile se numește hamiltonian.
• Graful care conține un ciclu hamiltonian se numește hamiltonian.

Condiție de suficiență

Dacă $G$ este un graf cu $n\ge 3$ noduri astfel încât gradul oricărui nod verifică inegalitatea $gr(x)\ge \frac{n}{2}$ rezultă că $G$ este graf hamiltonian. Este foarte rar folosită, nu se întâmplă des ca un graf hamiltonian să îndeplinească această condiție (este suficientă, nu necesară)

Graf neorientat eulerian

• Lanțul simplu care conține toate muchiile se numește eulerian.
• Ciclul simplu care conține toate muchiile se numește eulerian.
• Graful care conține un ciclu eulerian se numește eulerian.

Condiție necesară și suficientă

Un graf neorientat este eulerian dacă și numai dacă:

• Este conex
• Oricare nod al său are gradul par

Reprezentarea grafurilor neorientate

Matricea de adiacență

Pentru un graf neorientat $G=(V,E)$ cu $n$ noduri, matricea de adiacență $A$ este o matrice cu $n$ linii și $n$ coloane și elemente din $\{0,1\}$ (este booleană), cu $A_{i,j}=\{\begin{array}{ll}1& \text{daca˘ }(i,j)\in E\\ 0& \text{daca˘ }(i,j)\notin E\end{array}$ Exemplu: Pentru graful neorientat de mai jos avem următoarea matrice de adiacență: $A=\left(\begin{array}{ccccc}0& 1& 0& 0& 1\\ 1& 0& 0& 1& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 1\\ 1& 1& 0& 1& 0\end{array}\right)$

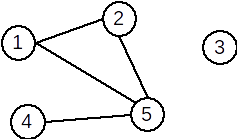
Observații

• matricea de adiacență este simetrică față de diagonala principală;
• elementele de pe diagonala principală sunt 0;
• gradul unui nod x este egal cu numărul de elemente 1 de pe linia (sau coloana) x;
• suma tuturor elementelor din matricea de adiacență a unui graf neorientat este egală cu dublul numărului de muchii din graf.

Lista de muchii

Lista de muchii a unui graf neorientat reprezintă o mulțime ce conține toate muchiile din graf.

Pentru graful de mai jos, lista de muchii este: 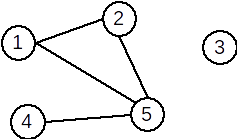$E=\{(1,2),(1,5),(2,5),(4,5)\}$ Atenție: în lista de muchii nu sunt reprezentate nodurile izolate.

Reprezentare în memorie

Pentru reprezentarea în memorie putem folosi:

• un tablou unidimensional cu elemente de tip struct {int I,J;}
• două tablouri unidimensionale cu elemente de tip int
• o listă alocată dinamic
• etc.

Liste de adiacențe

Pentru un graf neorientat cu $G=(V,E)$ se va memora numărul de noduri $n$ și apoi, pentru fiecare nod $x$, lista vârfurilor adiacente cu $x$, adică a nodurilor $y$ cu proprietatea că există muchia $(x,y)\in E$.

Pentru graful de mai jos, listele de adiacență sunt:

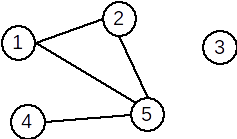
1: 2 5
2: 1 5
3: vidă
4: 5
5: 1 2 4

Reprezentarea în memorie

La reprezentarea în memorie trebui avut în vedere că dimensiunile listelor de vecini sunt variabile. De aceea, este ineficientă (dar posibilă cu o matrice de n linii și n-1 coloane) utilizarea unor tablouri alocate static. Astfel, putem folosi:

• un șir de n tablouri unidimensionale alocate dinamic;
• un șir de n vectori din STL;
• un șir de n liste simplu (dublu) înlănțuite alocate dinamic.